신뢰구간 구하는 방법

https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR

Auto Clicker - SmartNFast – Apps on Google Play

신뢰구간 구하는 방법

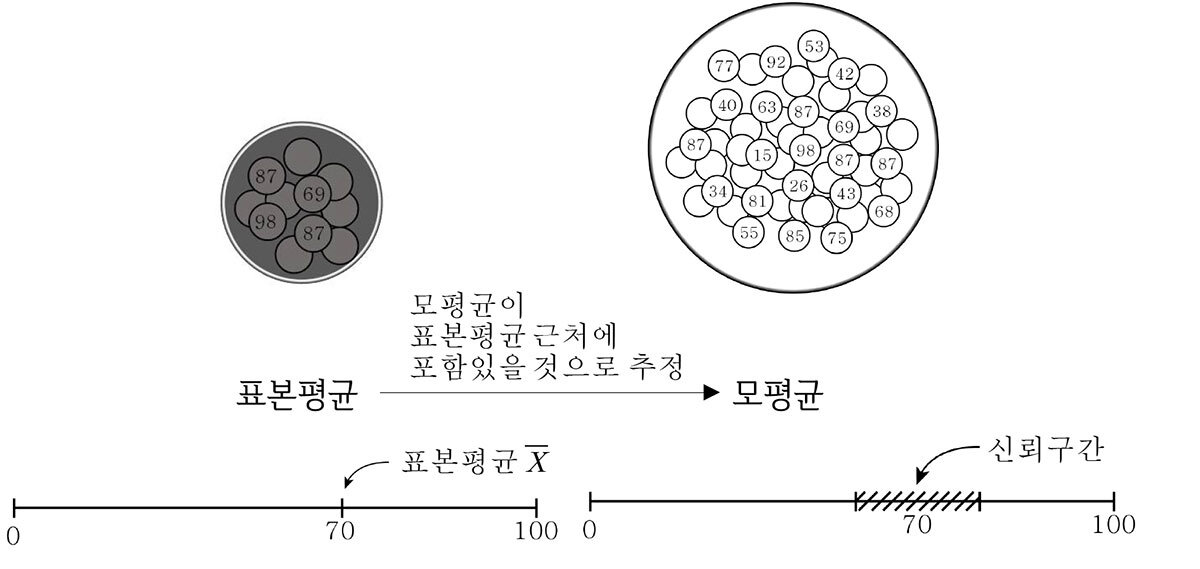
표본의 특성이 곧 모집단의 특성일 것임을 추정하며, 추정은 ‘구간’이나 ‘범위’로 가능하다. 표본의 평균을

라고 한다면

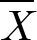
의 근처에서 모평균이 포함되어 있을 것이라는 강한 의심을 할 수 있다. 어디까지나 추정이므로 반드시 그 구간 내에 모평균이 포함된다고 할 수 없다. 이때 의심의 정도를 신뢰도라고 한다. 보통 신뢰도 95% 또는 99%에서 신뢰구간을 만든다. 95%정도로 표본평균과 그 근처인 신뢰구간 내에 모평균이 포함되어 있다는 것을 의심할 정도면 합리적인 의심이며 설령 그 범위를 벗어난다고 하더라도 크게 벗어나지 않을 것이라는 믿음이 있게 된다.

신뢰도가 높으면 신뢰구간이 넓어지며, 신뢰도가 낮으면 신뢰구간도 좁아지게 된다. 이처럼 신뢰도와 신뢰구간은 비례관계에 있다. 가령 100% 신뢰할 수 있는 신뢰구간이 있다면 전범위가 될 것이기 때문이다.

​

신뢰구간을 만드는 과정은 표준정규분포곡선에서 출발한다. 표준정규분포곡선 전체의 넓이는 1이며 1은 확률상 100%의 가능성을 의미한다. 그렇다면 95%의 가능성은 0.95의 넓이를 말한다. 이 넓이가 바로 신뢰도가 되며 신뢰도를 미리 ‘고정’시킨다.

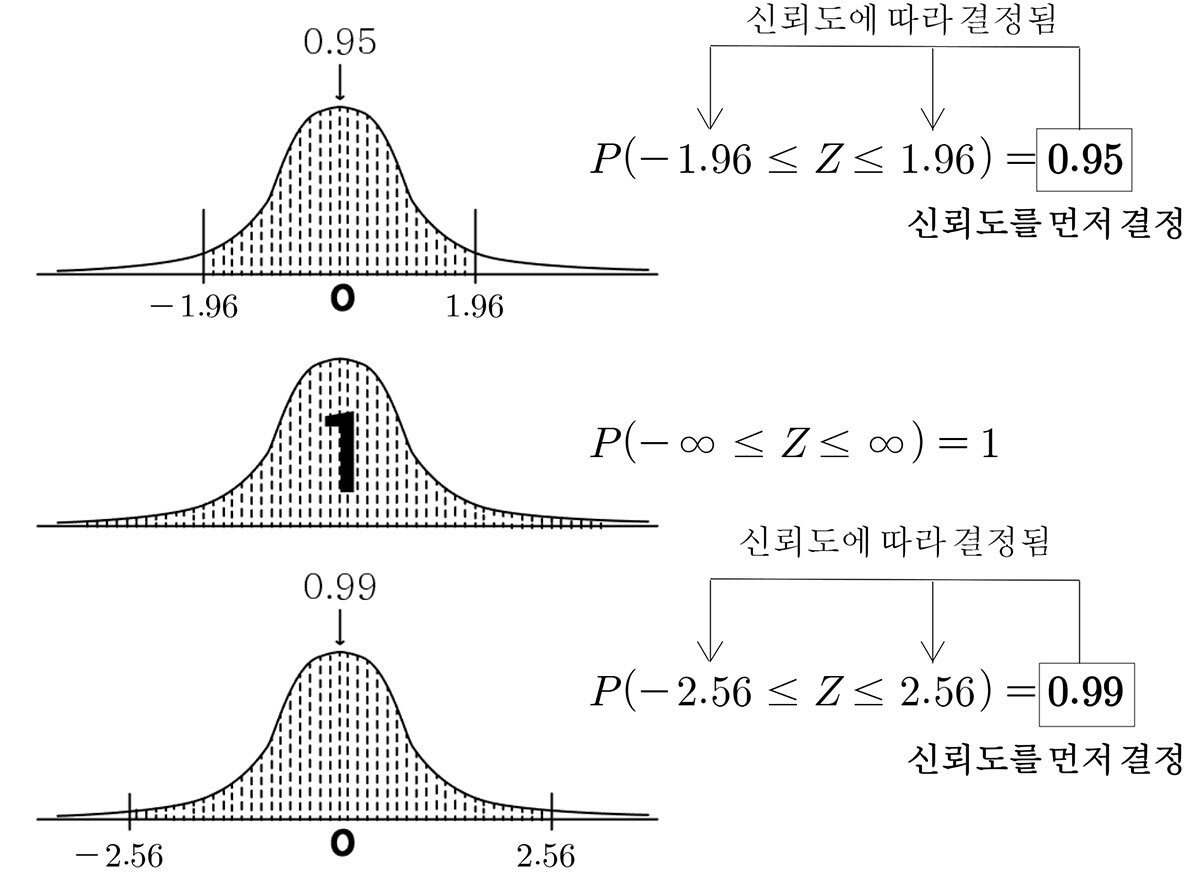
신뢰도 95% 에서 신뢰구간을 만들어보자.

− 1.96 ≤ Z ≤ 1.96이 신뢰구간이 아님을 주의하자. 이 식에서 Z는 표준화가 된 식이며 이때 표준화가 되기 이전의 식, 역표준화식으로 바꿔야 한다.

모집단의 확률변수 X의 평균과 표준편차가 m, σ일 때에서 표준화란

이며 표본평균

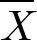
에 있어서 평균과 표준편차는 m과

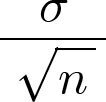
이므로 표본평균

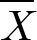
의 표준화란

 

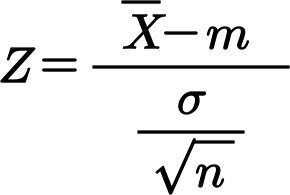
이다.

​

​

이 식에서 중요한 포인트는 모평균 m이 등장한다는 것이다. 이 식에서 모평균을 남겨두고 식을 변형하는 것이 포인트이다. 그게 바로 모평균 m이 95%이 확률로 속해질 범위 즉, 신뢰구간이 되는 것이다.

​

이러한 과정을 그림으로 표현하면 다음과 같다.

https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR

Auto Clicker - SmartNFast – Apps on Google Play